Se coloca una tuerca con una llave como se muestra en la figura. Si el brazo r es igual
a 30 cm y el torque de apriete recomendado para la tuerca es de 30 Nm, ¿cuál debe
ser el valor de la fuerza F aplicada?
.
Solución:
Σ t = r x F = 0,3 m x F = 30 Nm
Despejando:
0,3 m x F = 30 Nm
F = 30 Nm /0,3m
F = 100 N
La Física en la vida Cotidiana
viernes, 6 de noviembre de 2015
Momento de Torque y Fuerza
Cuando se aplica una fuerza en algún punto de un cuerpo rígido, dicho cuerpo tiende a realizar un movimiento de rotación en torno a algún eje.
Ahora bien, la propiedad de la fuerza aplicada para hacer girar al cuerpo se mide con una magnitud física que llamamos torque o momento de la fuerza.
Entonces, se llama torque o momento de una fuerza a la capacidad de dicha fuerza para producir un giro o rotación alrededor de un punto.
En el caso específico de una fuerza que produce un giro o una rotación, muchos prefieren usar el nombre torque y no momento, porque este último lo emplean para referirse al momento lineal de una fuerza.
Para explicar gráficamente el concepto de torque, cuando se gira algo, tal como una puerta, se está aplicando una fuerza rotacional. Esa fuerza rotacional es la que se denomina torque o momento.
Cuando empujas una puerta, ésta gira alrededor de las bisagras. Pero en el giro de la puerta vemos que intervienen tanto la intensidad de la fuerza como su distancia de aplicación respecto a la línea de las bisagras.
Entonces, considerando estos dos elementos, intensidad de la fuerza y distancia de aplicación desde su eje, el momento de una fuerza es, matemáticamente, igual al producto de la intensidad de la fuerza (módulo) por la distancia desde el punto de aplicación de la fuerza hasta el eje de giro.
M = F • d
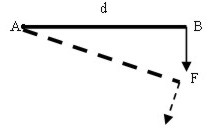 |
| Cuando se ejerce una fuerza F en el punto B de la barra, la barra gira alrededor del punto A. El momento de la fuerza F vale M = F • d |
donde M es momento o torque
F = fuerza aplicada
d = distancia al eje de giro
El torque se expresa en unidades de fuerza-distancia, se mide comúnmente en Newton metro (Nm).
Si en la figura de la izquierda la fuerza F vale 15 N y la distancia d mide 8 m, el momento de la fuerza vale:
M = F • d = 15 N • 8 m = 120 Nm
La distancia d recibe el nombre de “brazo de la fuerza”.
Una aplicación práctica del momento de una fuerza es la llave mecánica (ya sea inglesa o francesa) que se utiliza para apretar tuercas y elementos similares. Cuanto más largo sea el mango (brazo) de la llave, más fácil es apretar o aflojar las tuercas.
Ejemplo
Un patinador de 80 kg de masa le aplica a otro de 50 kg de masa una fuerza de 25 kgf durante 0,5 s, ¿qué velocidad de retroceso adquiere el primero y que velocidad final toma el segundo?.
Desarrollo
Datos:
m1 = 80 kg
m2 = 50 kg
F = 25 kgf = 25 kgf.9,8.665 N/1 kgf = 245,17 N
t = 0,5 s
Según la definición de impulso:
I = F.t
I = 245,17 N.0,5 s
I = 122,58 kg.m/s
I = 245,17 N.0,5 s
I = 122,58 kg.m/s
El impulso en el momento del choque es el mismo para ambos cuerpos y el impulso también es igual a la cantidad de movimiento.
I = m1.v1
I/m1 = v1
v1 = (122,58 kg.m/s)/80 kg
v1 = 1,53 m/s
I/m1 = v1
v1 = (122,58 kg.m/s)/80 kg
v1 = 1,53 m/s
I = m2.v2
I/m2 = v2
v2 = (122,58 kg.m/s)/50 kg
v2 = 2,45 m/s
I/m2 = v2
v2 = (122,58 kg.m/s)/50 kg
v2 = 2,45 m/s
Impulso y cantidad de movimiento
Impulso
El impulso es el producto entre una fuerza y el tiempo durante el cual está aplicada. Es una magnitud vectorial. El módulo del impulso se representa como el área bajo la curva de la fuerza en el tiempo, por lo tanto si la fuerza es constante el impulso se calcula multiplicando la F por Δt, mientras que si no lo es se calcula integrando la fuerza entre los instantes de tiempo entre los que se quiera conocer el impulso. |  |


Cantidad de Movimiento
La cantidad de movimiento es el producto de la velocidad por la masa. La velocidad es un vector mientras que la masa es un escalar. Como resultado obtenemos un vector con la misma dirección y sentido que la velocidad.La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.

m = Masa
v = Velocidad (en forma vectorial)
p = Vector cantidad de movimiento
Relación entre Impulso y Cantidad de Movimiento
El impulso aplicado a un cuerpo es igual a la variación de la cantidad de movimiento, por lo cual el impulso también puede calcularse como:
Dado que el impulso es igual a la fuerza por el tiempo, una fuerza aplicada durante un tiempo provoca una determinada variación en la cantidad de movimiento, independientemente de su masa:

Ejemplo
Calcula la fuerza obtenida en el émbolo mayor de una prensa hidráulica si en el menor se hacen
15N y los émbolos circulares tienen cuádruple radio uno del otro.
Calcula la fuerza obtenida en el émbolo mayor de una prensa hidráulica si en el menor se hacen
15N y los émbolos circulares tienen cuádruple radio uno del otro.
Muy parecido al anterior, y si parece que faltan datos es porque no nos hacen falta. Vamos a
sustituir lo que sabemos en la fórmula del principio de Pascal:
F1 = 15N
F2 = ?
S1 = π·R1
2
(no podemos sustituir nada, así que lo dejamos así)
S2 = π·R2
2
= π·(4R1)
2
= π· 16R1
2
F1/S1 = F2/S2
15/π·R1
2 = F2/π·16R1
2
Simplificamos
15/1 = F2/16
F2 = 15·16 = 240N
Calcula la fuerza obtenida en el émbolo mayor de una prensa hidráulica si en el menor se hacen
15N y los émbolos circulares tienen cuádruple radio uno del otro.
Muy parecido al anterior, y si parece que faltan datos es porque no nos hacen falta. Vamos a
sustituir lo que sabemos en la fórmula del principio de Pascal:
F1 = 15N
F2 = ?
S1 = π·R1
2
(no podemos sustituir nada, así que lo dejamos así)
S2 = π·R2
2
= π·(4R1)
2
= π· 16R1
2
F1/S1 = F2/S2
15/π·R1
2 = F2/π·16R1
2
Simplificamos
15/1 = F2/16
F2 = 15·16 = 240N
Principio de Pascal
En física, el principio de Pascal o ley de Pascal, es una ley enunciada por el físico y matemático francés Blaise Pascal (1623-1662) que se resume en la frase: la presión ejercida en cualquier lugar de un fluido encerrado e incompresible se transmite por igual en todas las direcciones en todo el fluido, es decir, la presión en todo el fluido es constante.
La presión en todo el fluido es constante: esta frase que resume de forma tan breve y concisa la ley de Pascal da por supuesto que el fluido está encerrado en algún recipiente, que el fluido es incompresible... El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el émbolo, se observa que el agua sale por todos los agujeros con la misma presión.
También podemos ver aplicaciones del principio de Pascal en las prensas hidráulicas.
aplicación de principio de pascal
El principio de Pascal puede ser interpretado como una consecuencia de la ecuación fundamental de la hidrostática y del carácter altamente incompresible de los liquidos. En esta clase de fluidos la densidad es prácticamente constante, de modo que de acuerdo con la ecuación:
Donde:
, presión total a la profundidad
medida en Pascales (Pa).
, presión sobre la superficie libre del fluido.
, densidad del fluido.
, aceleración de la gravedad.
Si se aumenta la presión sobre la superficie libre, por ejemplo, la presión total en el fondo ha de aumentar en la misma medida, ya que el término ρgh no varía al no hacerlo la presión total (obviamente si el fluido fuera compresible, la densidad del fluido respondería a los cambios de presión y el principio de Pascal no podría cumplirse)
La presión en todo el fluido es constante: esta frase que resume de forma tan breve y concisa la ley de Pascal da por supuesto que el fluido está encerrado en algún recipiente, que el fluido es incompresible... El principio de Pascal puede comprobarse utilizando una esfera hueca, perforada en diferentes lugares y provista de un émbolo. Al llenar la esfera con agua y ejercer presión sobre ella mediante el émbolo, se observa que el agua sale por todos los agujeros con la misma presión.
También podemos ver aplicaciones del principio de Pascal en las prensas hidráulicas.
aplicación de principio de pascal
El principio de Pascal puede ser interpretado como una consecuencia de la ecuación fundamental de la hidrostática y del carácter altamente incompresible de los liquidos. En esta clase de fluidos la densidad es prácticamente constante, de modo que de acuerdo con la ecuación:
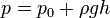 |
| p = p_0 + rho g h , |
Donde:
 |
| p , |
 |
| h , |
 |
| p_0 , |
 |
| rho , |
 |
| g , |
Si se aumenta la presión sobre la superficie libre, por ejemplo, la presión total en el fondo ha de aumentar en la misma medida, ya que el término ρgh no varía al no hacerlo la presión total (obviamente si el fluido fuera compresible, la densidad del fluido respondería a los cambios de presión y el principio de Pascal no podría cumplirse)
Ejemplo
Practica:
Fext=0 Fext=dPdt P=cte

Desde el extremo de una plataforma móvil de 80 kg, inicialmente en reposo, un niño de 40 kg corre hacia el otro extremo a una velocidad constante de 1 m/s (respecto de la plataforma). Determinar la velocidad de la plataforma y el sentido de su movimiento. ¿Qué principio físico aplicas?
Solución
Sistema aislado
Principio de conservación del momento lineal. El momento lineal inicial es cero, (el niño está en reposo sobre la plataforma).

El niño empieza a correr con velocidad de 1 m/s respecto a la plataforma, es decir, con velocidad (1+v) respecto de Tierra, siendo v la velocidad de la plataforma.
0=40(1+v)+80·v
v=-1/3 m/s
v=-1/3 m/s
El niño se mueve hacia la derecha y la plataforma se mueve hacia la izquierda
Suscribirse a:
Comentarios (Atom)